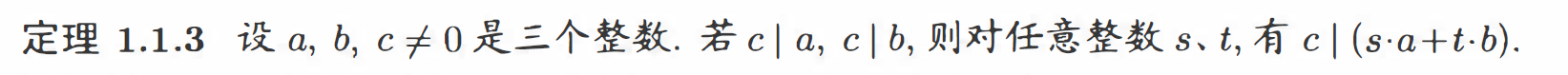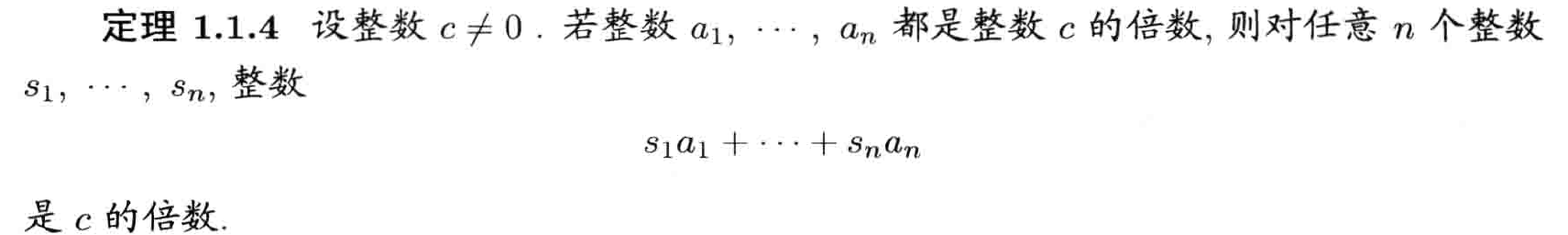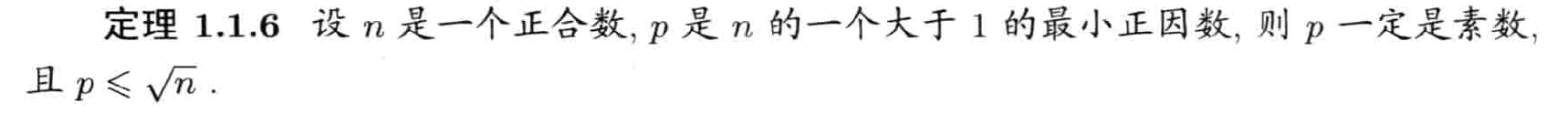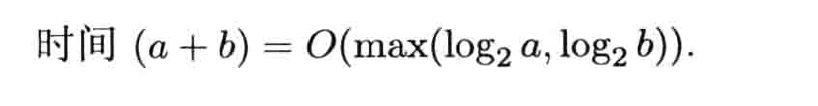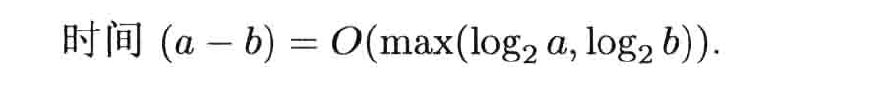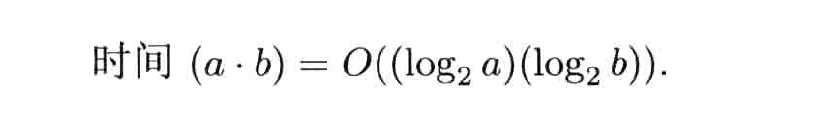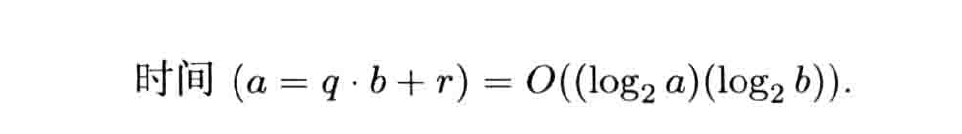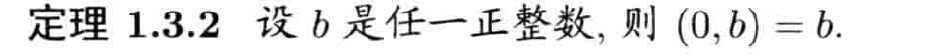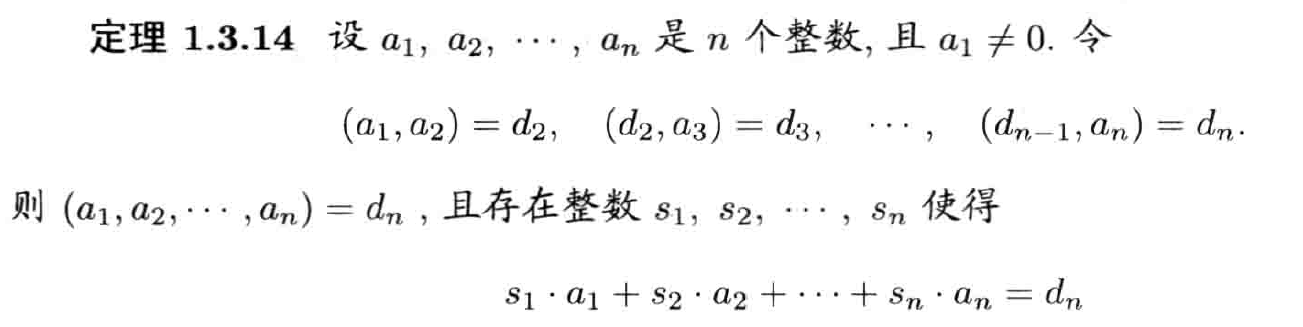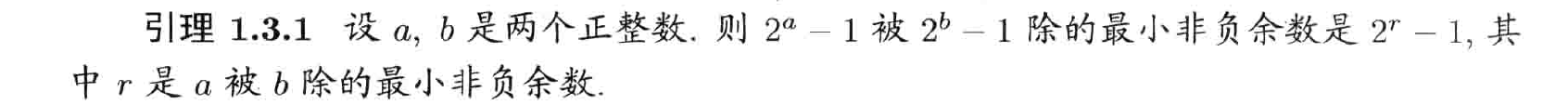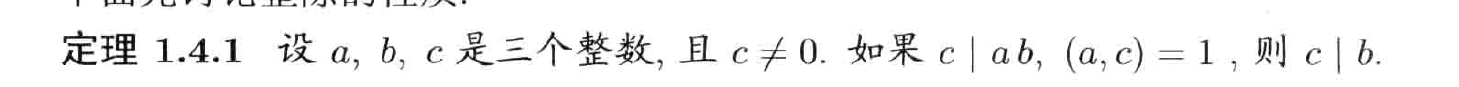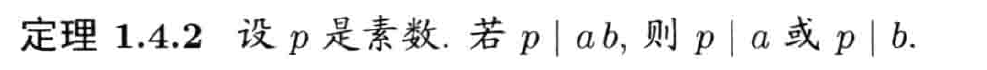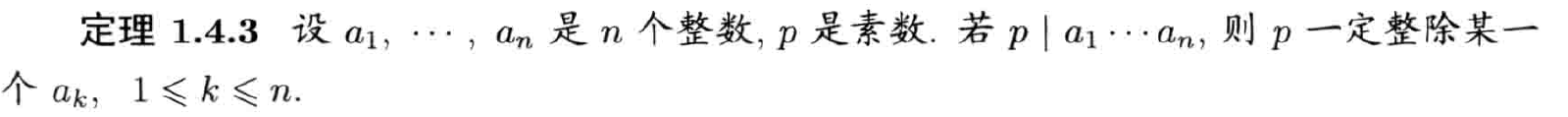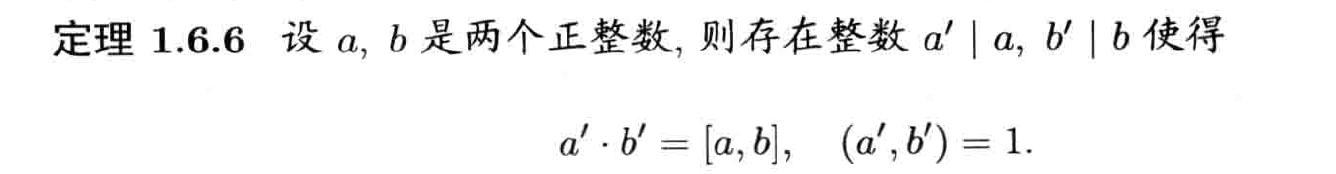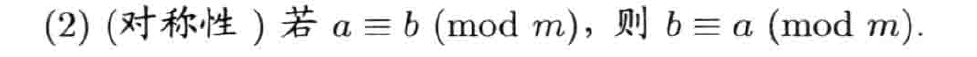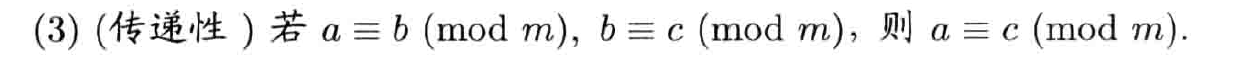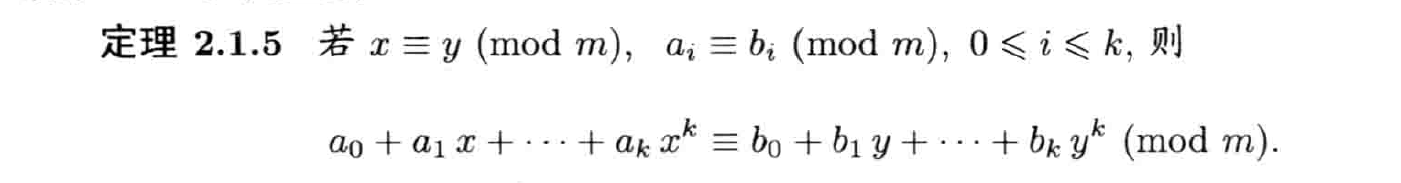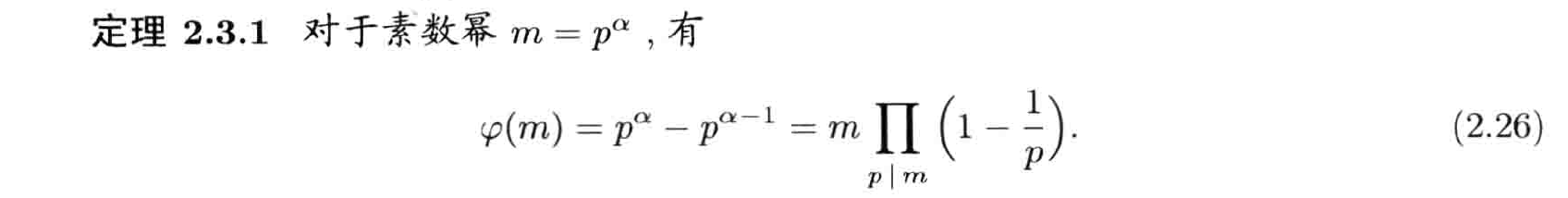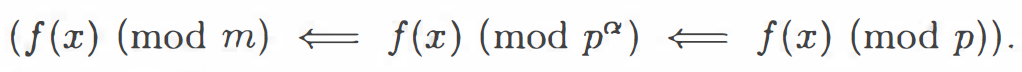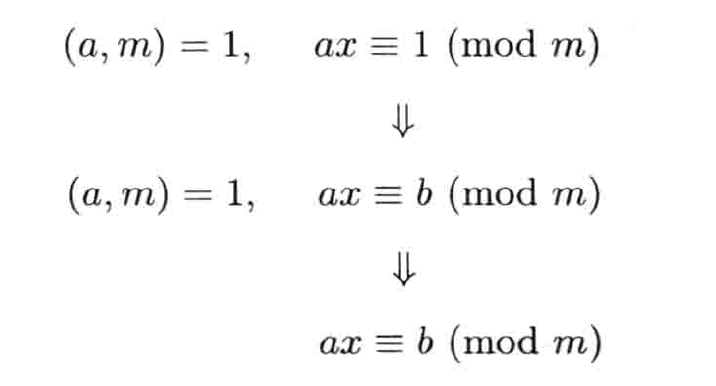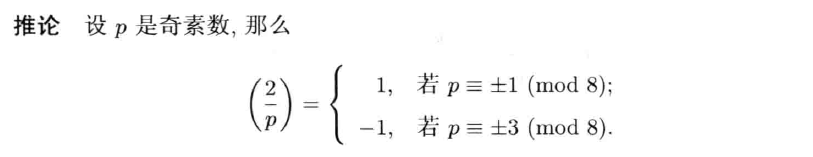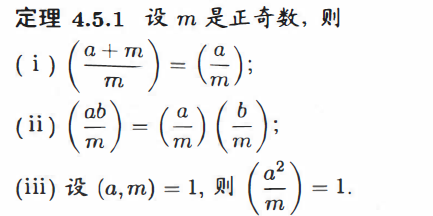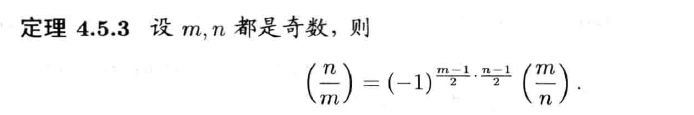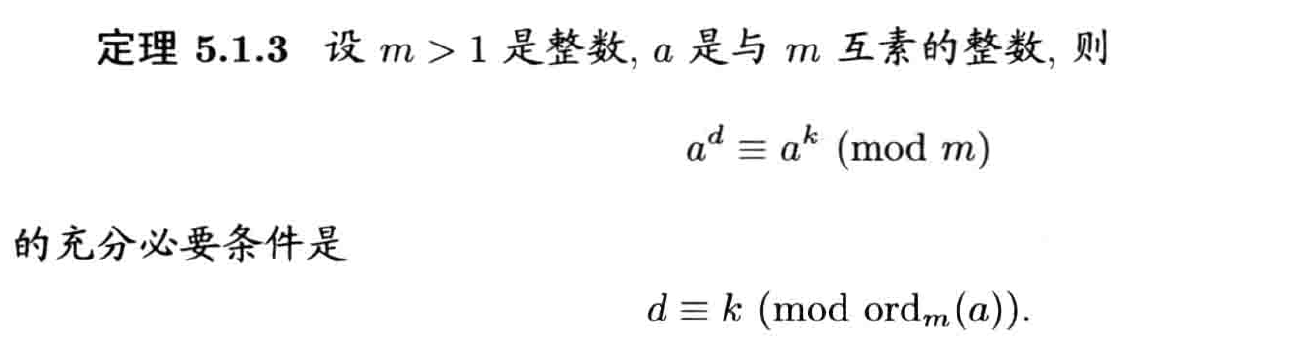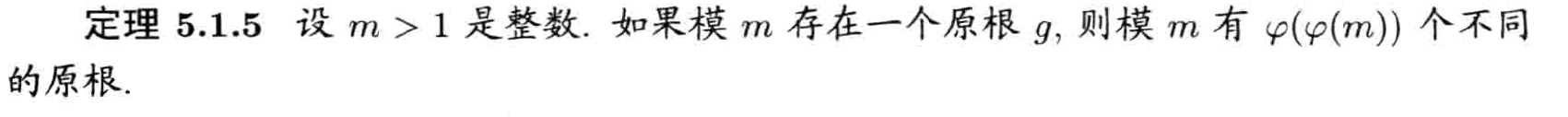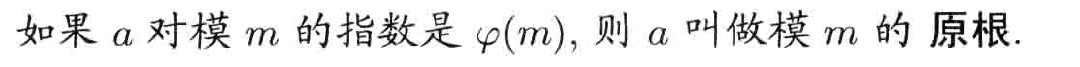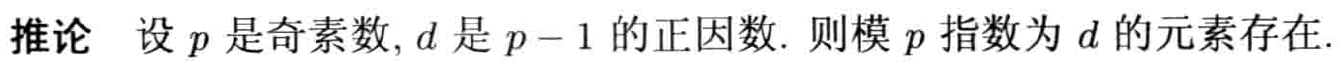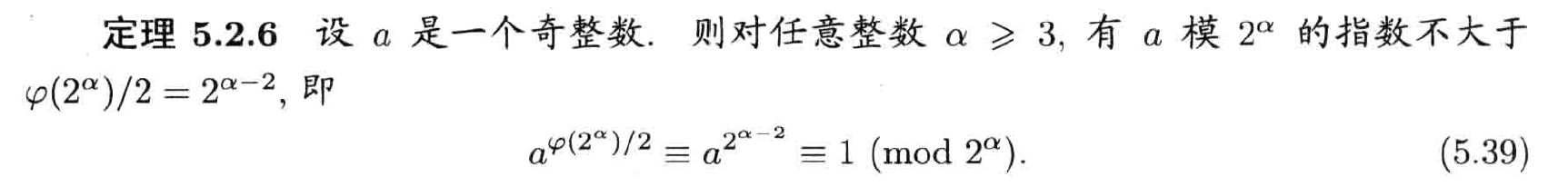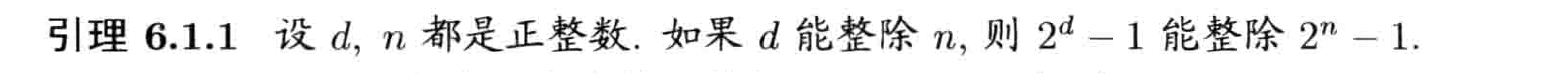密码学数论数学

数学

发布日期: 2022-04-01

更新日期: 2022-04-25

文章字数: 1.8k

阅读次数:

数论

整数

整除

定义
性质
- 特性
  - (1）当b遍历整数a的所有因数时，－b 也遍历整数a的所有因数
  - （2）当b遍历整数 a的所有因数时，a/b 也遍历整数a的所有因数
  - (3) 0是任何非零整数的倍数．
  - (4) 1是任何整数的因数
  - (5) 任何非零整数α 是其自身的倍数,也是其自身的因数
- 传递性
- 加减保持性
- 线性组合性
- 互逆

素数

定义
筛选法
- Eratoshenes筛法引理
- Eratoshenes筛法
性质
- 无穷性
  - 素数有无穷多个

欧几里得除法

定义
- 补充
素数平凡判别法
一般余数定义
- 延拓余数形式
  - 例题

整数的表示（多项式）

b进制表示（多项式形式）
- 定义
  - 详细
- 转换
  - 这里不多介绍，除取余法
- 运算（多项式类似）
  - 加法
  - 减法
  - 乘法
  - 除法（欧式空间下除法）
复杂度（极限下无穷量）
- 大O符号
- 小o符号
- 运算
  - 加法
  - 减法
  - 乘法
  - 除法

最大公因数

定义
- 补充
性质
- 相等
- 0性
- 欧几里得除法引理

广义欧几里得除法

定义（辗转相除法）
- 例如
  - - 绝对值最小余数可以快速下降化解
性质
贝祖等式
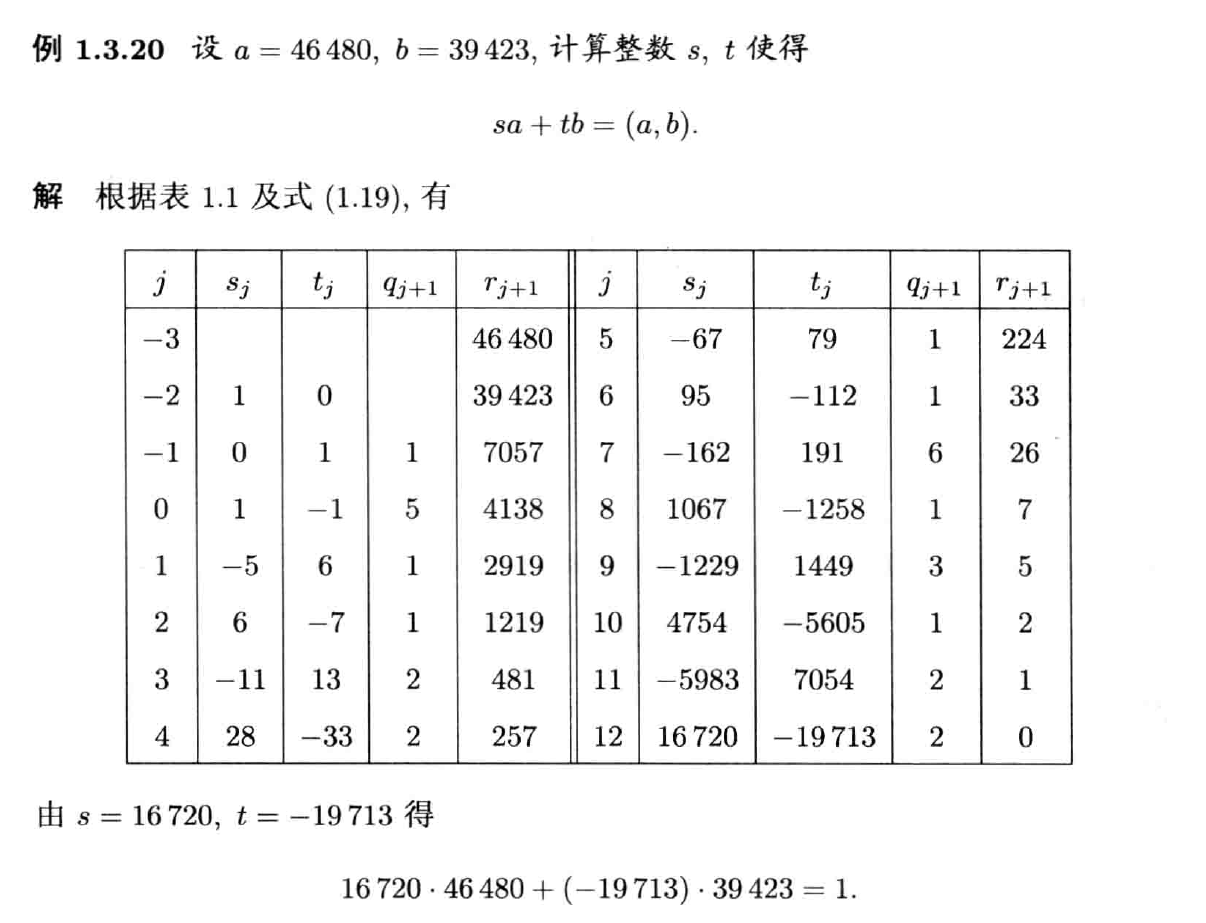
- 例如
证明
应用

最大公因数

互素定义
最大公因数定义
推论
- 素数构造
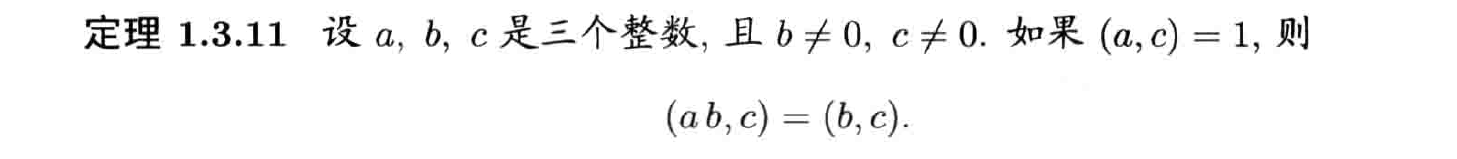
- - 可以写成行列式形式
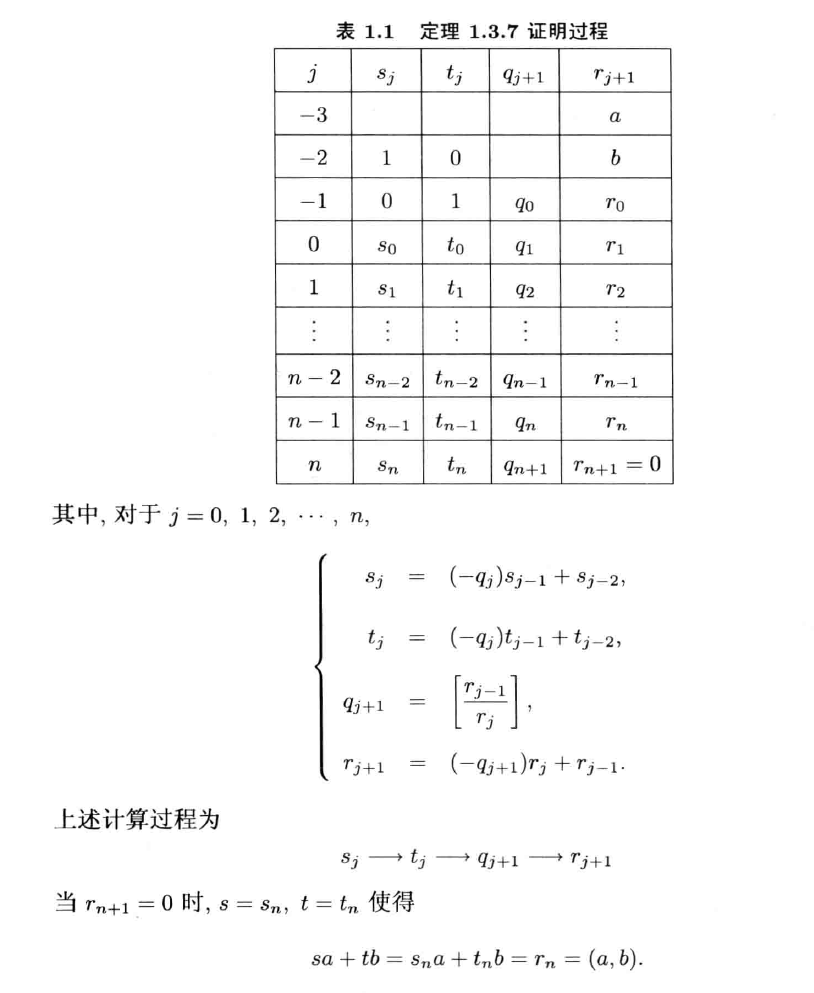
计算定理
- 线性递推
- 指数

最小公倍数

前提引理推论（整数性质扩展）
定义
最小公倍数与最大公因数的关系
拓展多个

整数分解

整数分解定理
例题

素数算术基本定理(多项式形式重根)

算术基本定理
- 这里素数乘积，表示素数开始作为空间的基，了解素数就可以掌握这个空间映射
标准分解式（加入重根）
因式分解
- 素数组合
最大公因数额最小公倍数的内涵
- 推论
- 推论n个
特殊结论
素数定理
切比谢夫不等式
- - 素数位置估计

同余

概念
判断原理
等价关系的性质
- 自反
- 对称
- 传递
推论
- 余数相同判定
特性
- 相加相乘（满足线性空间）
- 空间相等
- 3，9特性
  - - 小时候用的估算
- 7,11,13特性
  - - 差分估计
性质
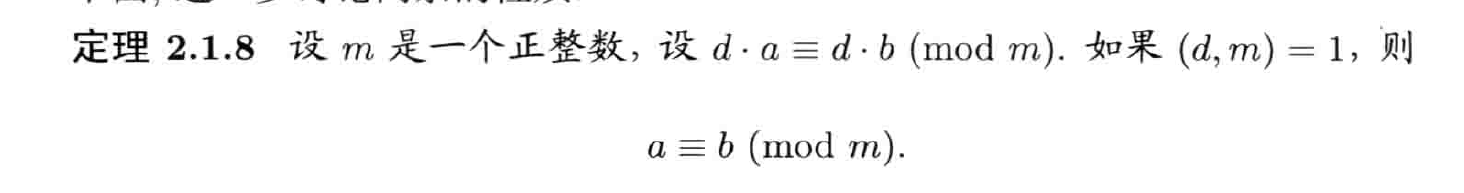
- - 换成整除证明

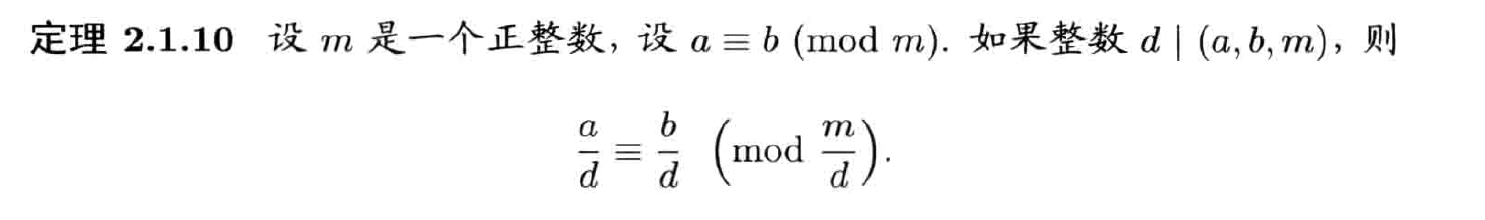
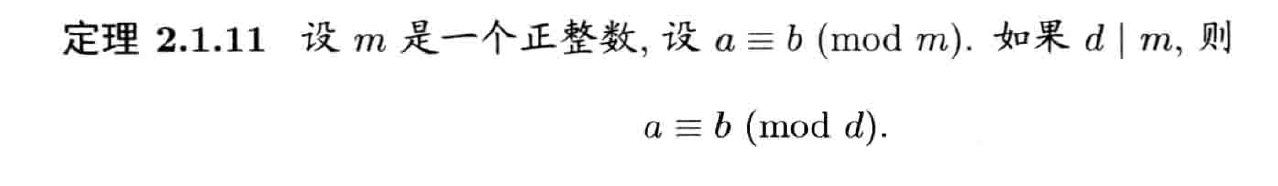
剩余类

定义前提
完全剩余类
- 定义
- 性质
- 判定定理
- 类型
- 遍历
  - 同理推广n维
简化剩余类
- 定义
- 互素
- 简化剩余系
  - 定义
  - 类型
- 遍历

欧拉函数

定义
欧拉定理
性质
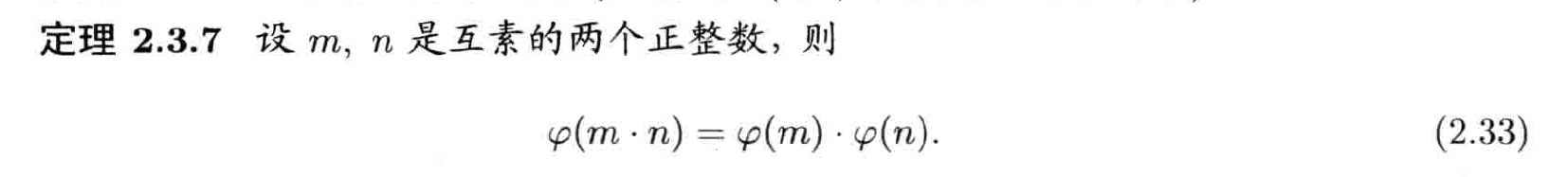
- 计算方法
- 推论
- 原根的构建

经典定理

欧拉定理
- 推论
费马小定理
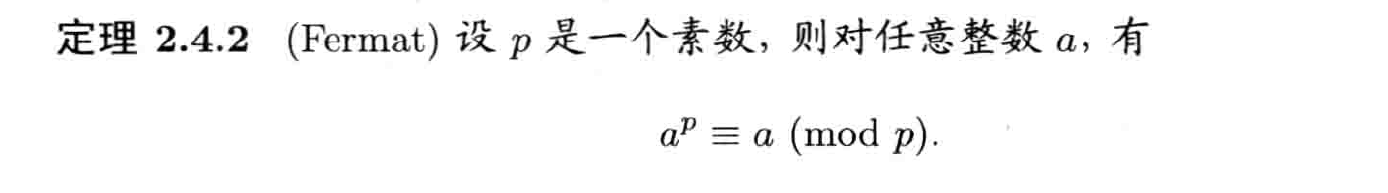
- 推论
Wilson定理

模重复

思想
方法
- 例题见书

同余式

定义
- 解空间（剩余类）
  - 类比高数中微分方程的解空间和代数空间下的解空间，同构罢了
基本思路
- (1）求解归约 (J(x) (mod m）仨＝ f(x) (mod pa) <== f(x) (mod p)).
- (2）解的存在性（如定理3.1.1).
- (3）解的个数（如定理3.1.3，定理3.4.4，定理3.4.5).
- (4）具体求解（如定理3.2.1，定理3.4.1).
一次同余式求解过程
- 思路
- 相关定理
  - 存在性证明
  - 解个数
  - 代数可逆补充
    - 可逆元（这个没必要吧，前面涉及到了）
    - 简化剩余类可逆元遍历（这里就是想法上一个转化，转化为求可逆元，利用前面的同余以及辗转相除法）
- 例题
  - 思路：和微分方程一样，先判断有解，然后求解特解，再求解空间

中国剩余定理

定理**
- 俩种表示形式，个人更偏向第一种好记忆，第二种偏递推得出的结论，适合证明
2个方程版
- （其实和上面差不多只是加了辗转相除法简化了一下，其实我感觉一模一样）
推广
- 遍历（这个我其实不太懂）
- 类似上面吧
例题（详细看书吧）

高次同余式

解法
- 常见的转化，化为同余式组
  - 这里应该和代数空间上分解有关
- 例题
提升
- 定义
  - 总感觉和不可约多项式那边有点像
- 解法

素数模的同余式（这个有用）

多项式除法（代数学过）
简化
因式分解
解法
- 判定定理
- 上界估计
- 解数判断
- 推论

二次同余式与平方剩余

定义

二次同余式
平方剩余

模p为奇素数的判别法

欧拉判别法
- 推论
- 二次平方剩余系
勒让得符号
- 定理
- 性质
- 子主题 3
相关定理
高斯引理
- 推论
- 求解定理
二次互反律
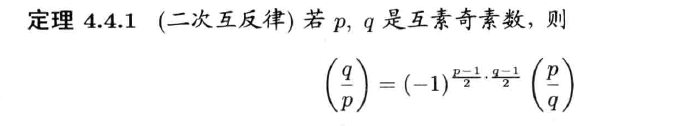
- 辅助
雅可比符号
- 弱化条件
  - 在勒让得符号的计算中，要求模p为素数此外，在二次互反律的应用中，也要求α＝q为素数．这些都是很强的条件，因此，希望这些条件可以弱化，只要求模m为奇整数，α为任意整数．
- 定义
- 定理
- 引理
- 推论
- 二次互反

模平方根

具体求解
模 p 平方根
- 设p是形为4k +3的素数．讨论此情形的模p平方根
- 证明
模p平方根
- p为奇素数
- 解定理
模m平方根
- 条件
- 解定理
  - p^a
    - 推论
  - a的分情况
x^2+y^2 = p
- 定理

原根与指标

这一章应该算代数数论了，初等数论只涉及一点点

指数（阶）

定义
基本性质
- 这里揭示了域的同构
- 推论欧拉定理可得
- 还是欧拉变形
- 同构下性质保持不变
- 这个不清楚，应该是同构映射基类似吧
- 计算与优化
- 同构
- 构造
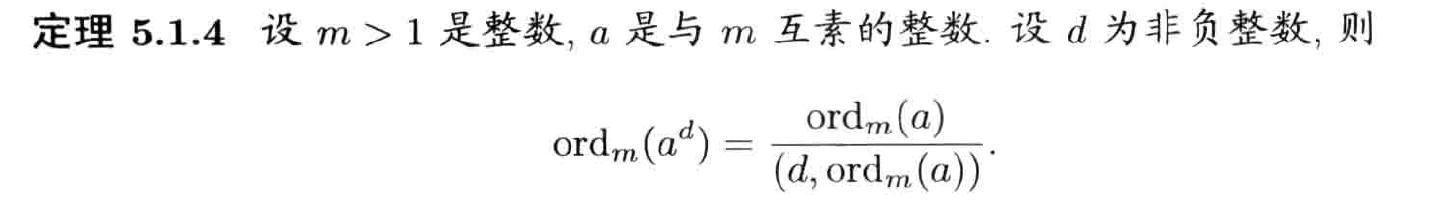
  - 推论
重要定理
大指数构造（感觉就是同构后的性质和前面一样）
- 互素相乘
- 揭露了阶的含义，最大公倍数，这里就可以看成域的自乘了
  - 推论
- 关系
  - 引理